WolframAlpha Chatbot Integration

Tired of AI

Get Factual Responses Every Time

Pro Members

What is Wolfram Alpha?

Wolfram Alpha (aka WoframAlpha or Wolfram|Alpha) is a unique computational knowledge engine developed by Wolfram Research. It is designed to provide answers to factual queries by computing the answer from externally sourced “curated data”, rather than providing a list of documents or web pages that might contain the answer as a search engine might. It covers a vast array of subjects, providing precise computations, definitions, and data analysis.

How the Integration Works

ClassX Pro now uses Wolfram Alpha right inside its chatbot. Whenever you ask a question that needs detailed calculations or exact facts, both the chatbot and Wolfram Alpha work together to give you the answer. This means you get answers that not only make sense but are also correct and backed by math. Plus, you can keep asking more questions and get factual answers right away, all in the same chat.

Step 1: Click on the Wolfram Alpha Icon

To access the WolframAlpha chatbot, click on the red Wolfram icon.

Step 2: Ask a Question or Upload a Picture

Ask a question or upload a picture of the question.

Step 3: Discuss the answer

When you press the send button, the chatbot will automatically check if the answer can be computed by Wolfram Alpha. If so, Wolfram Alpha will provide the answer straight into the chatbot for further discussion.

Benefits of Using Wolfram Alpha Integration for Homework Help

Accuracy: With Wolfram Alpha, you get super accurate answers for your homework questions. It’s like having a math genius at your fingertips!
Comprehensiveness: Whether you’re working on history, science, or math, you can dig into detailed data and calculations for all sorts of topics.
Efficiency: Get quick answers to complex problems right during your study session, saving you tons of time.
Instant Homework Help: Not only do you get correct answers quickly, but you can also ask follow-up questions and understand your homework better in real-time.

Benefits of Using Wolfram Alpha Integration for Teachers

Accuracy: Ensures that the information you provide to students is precise, helping them learn correctly.
Resourcefulness: Access a wide range of data and calculations to enrich lesson plans across various subjects.
Efficiency: Quickly find and verify answers during class discussions, saving valuable teaching time.
Interactive Learning: Facilitates engaging classroom interactions as students can ask follow-up questions and explore topics in real-time, enhancing their understanding and curiosity.

Compute expert-level answers using Wolfram’s breakthrough algorithms, knowledgebase and AI technology

Pro Membership

Get factual information every time with the Wolfram|Alpha integration. No matter which subject you’re studying (or teaching), our WolframAlpha integration gives you superpowers!

Login

Subjects

Mathematics

With the ClassX WolframAlpha integration, students and teachers can leverage the broad knowledge and deep computational power of WolframAlpha for a range of subjects, especially in math. Whether it’s arithmetic, algebra, calculus, differential equations, or anything in between, this integration is up to the challenge. Use it to get help with math homework, solve specific math problems, or find detailed information on mathematical subjects and topics.

Elementary Math

Wolfram|Alpha is great for advanced calculations, but it can also help with basic math problems. For example, it can solve arithmetic questions like addition and subtraction, convert fractions to decimals, and solve math word problems. It can also work with unknown values to figure out if a number is odd or even, positive or negative. For instance, it can tell if a number is positive even if you don’t know the exact number.

Elementary Math Fields

Perform multiple arithmetic operations.

Arithmetic

Perform arithmetic on fractions.

Fractions

Compute percentages or solve percentage increase/decrease problems.

Percentages

Explore place value charts for decimal numbers.

Place Value

Perform computations on signs, categories and types of numbers.

Number Type Arithmetic

Compute the answer and examine related facts for a math word problem.

Mathematical Word Problems

Examples:

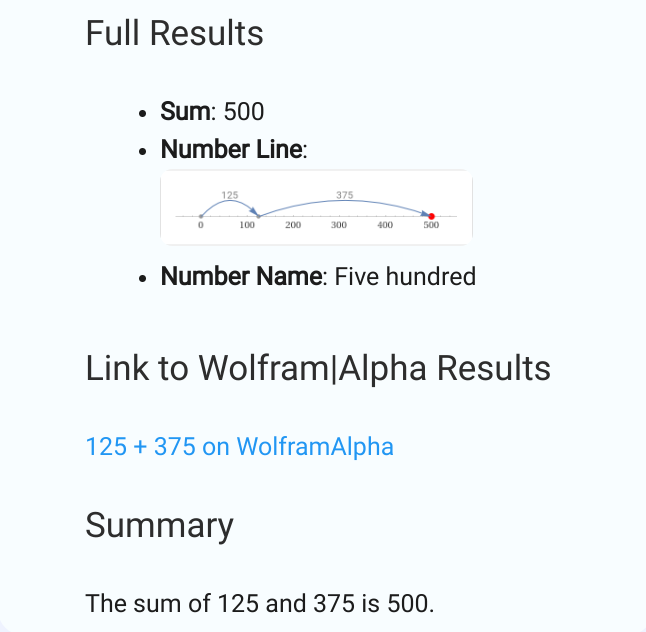
1. $23 + 57$

2. $89−34$

3. $12×8$

4. $144÷12$

Algebra

Algebra is a key area of mathematics focused on studying variables and the operations that apply to numbers and symbols. Wolfram|Alpha is an excellent tool for solving equations, exploring polynomials, and studying concepts such as fields, groups, vectors, and matrices. For instance, you can use it to solve quadratic equations, find the roots of a polynomial, or calculate the determinant of a matrix.

Algebra Fields

Solve equations in one or more variables both symbolically and numerically.

Equation Solving

Solve, plot and find alternate forms of polynomial expressions in one or more variables.

Polynomials

Compute discontinuities and other properties of rational functions.

Relational Functions

Simplify algebraic functions and expressions.

Simplification

Perform computations with the quaternion number system.

Quaternions

Discover properties of groups containing a finite number of elements.

Finite Groups

Find properties and perform computations on matrices.

Matrices

Discover properties of fields containing a finite number of elements.

Finite Fields

Find the domain and range of mathematical functions.

Domain & Range

Examples:

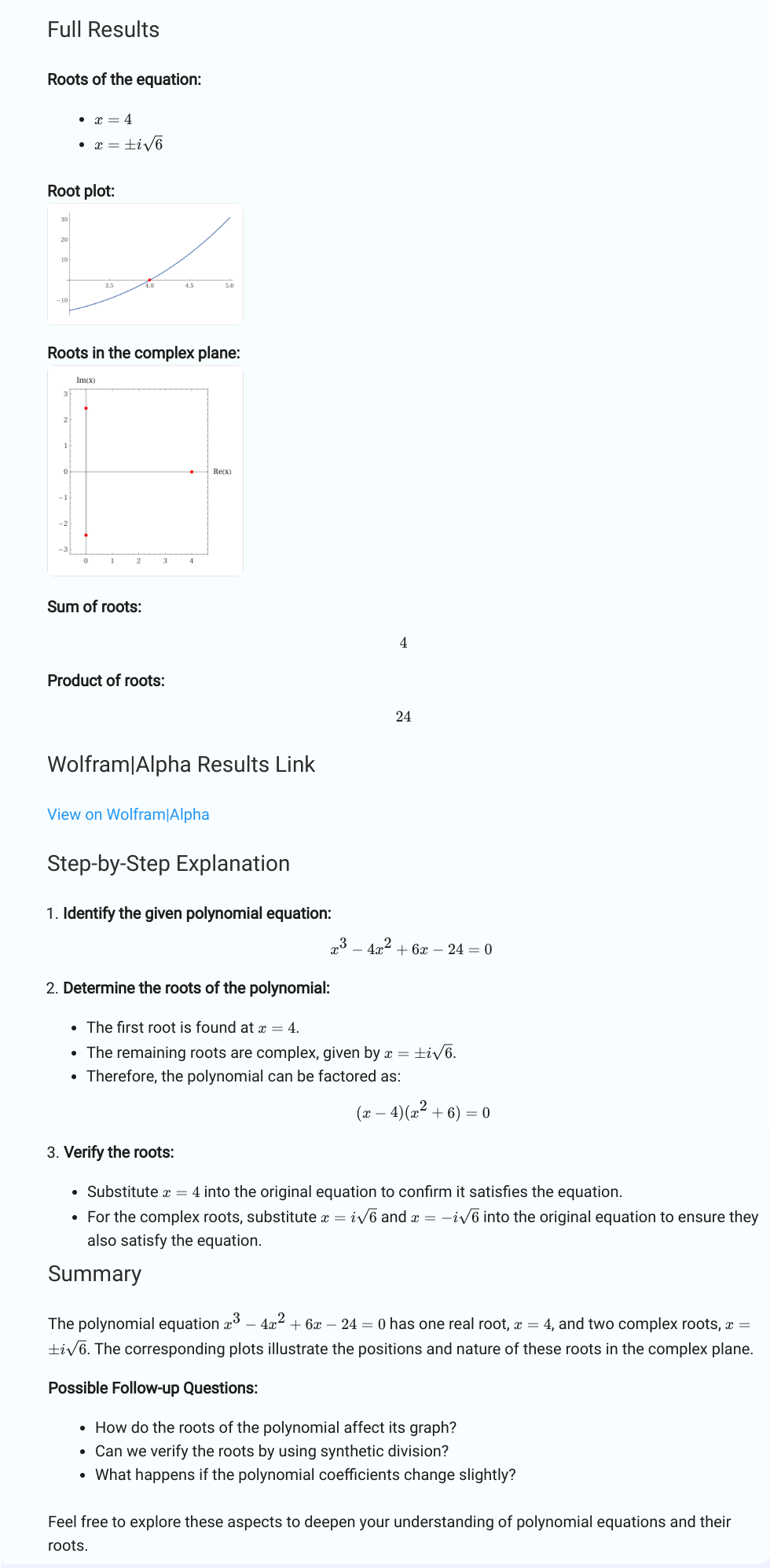
1. $2x + 3 = 7$

2. $frac{x^2 – 4}{x – 2}$

3. $(x + 2)^3$

4. $x^2 + 5x + 6$

Calculus & Analysis

Calculus is the branch of mathematics that studies how quantities change and measures the length, area, and volume of objects. Wolfram|Alpha is an excellent tool for answering questions in both single and multivariable calculus. It can compute limits, derivatives, and integrals, and apply these concepts to find tangent lines, extrema, arc lengths, and more. For example, you can use it to determine the derivative of a function, find the area under a curve, or solve a differential equation.

Calculus & Analysis Fields

Compute definite and indefinite integrals of functions. Integrate with respect to one or more variables.

Integrals

Take the derivative of single or multivariate functions. Compute the partial derivative of expressions with more than one variable.

Derivatives

Explore the limit behavior of a function as it approaches a single point or asymptotically approaches infinity.

Limits

Calculate and examine sequences of integers or other numerical values. Find continuations and formulas for known or unknown sequences.

Sequences

Compute an indexed product by multiplying a finite or infinite number of terms.

Products

Find Taylor series, Laurent series and more about any point.

Series Expansion

Compute the value of indexed summations, or sums of sequences of values. Compute infinite sums and find convergence conditions.

Sums

Apply the curl, the gradient and other differential operators to scalar and vector fields.

Vector Analysis

Calculate the Fourier transform, Laplace transform and other integral transforms of functions.

Integral Transforms

Use calculus tools, such as integrals and derivatives, to calculate properties of curves, surfaces, solids and planar regions.

Application of Calculus

Find discontinuities and continuous intervals of a function. Also determine whether particular discontinuities are removable or infinite due to an asymptote.

Continuity

Compute the domain and range of real mathematical functions. Plot the domain and range on a number line.

Domain & Range

Examples:

1.$frac{d}{dx} (x^3 – 3x^2 + 2x)$

2. $int (2x^2 + 3x + 1) dx$

3. $lim_{{x to 0}} frac{sin(x)}{x}$

4. $sum_{{n=1}}^{infty} frac{1}{n^2}$

Geometry

Geometry is the field of mathematics that studies the properties of shapes and the space they occupy. Wolfram|Alpha can analyze and compute with geometric figures of various dimensions, such as polygons and polyhedra. It can also solve practical problems using geometry, like tiling or packing problems. Additionally, Wolfram|Alpha can provide information on more advanced topics such as analytic geometry and topology. For example, you can use it to calculate the area of a triangle, determine the volume of a cylinder, or explore the properties of a dodecahedron.

Geometry Fields

Compute properties of 2D geometric figures.

Plane Geometry

Compute properties of 3D geometric figures.

Solid Geometry

Specify geometric figures by coordinates or algebraic equations.

Coordinate Geometry

Visualize and compute properties for different kinds of geometric transformations.

Geometric Transformations

Compute properties of geometric figures with dimensions higher than three.

High-Dimensional Geometry

Determine the optimal packing of geometric figures or generate estimates using real‐life objects.

Packing & Coverings Problems

Visualize and compute properties of curves and surfaces.

Curves & Surfaces

Visualize a moiré pattern.

Moiré Patterns

Compute properties of a class of polyforms.

Polyforms

Visualize both periodic and nonperiodic tilings.

Tilings

Compute topological properties for various kinds of geometric objects.

Topolgy

Examples:

1. Area of a circle with radius 5

2. Perimeter of a rectangle with length 10 and width 4

3. Volume of a sphere with radius 3

4. Angle between two intersecting lines

Differential Equations

A differential equation is an equation that involves a function and its derivatives. It can be called an ordinary differential equation (ODE) if it involves regular derivatives, or a partial differential equation (PDE) if it involves partial derivatives. Wolfram|Alpha can solve many problems in this important branch of mathematics, including solving ODEs, finding the ODE that a function satisfies, and solving an ODE using various numerical methods. For example, you can use it to model population growth, simulate heat distribution, or analyze electrical circuits.

Differential Equation Fields

Solve an ODE or find an ODE a function satisfies.

Ordinary Differential Equations

Use numerical methods to solve ordinary differential equations.

Numerical Differential Equation Solving

Examples:

1. Solve a linear ordinary differential equation:

$y” + y = 0$

2. Specify initial values:

$y” + y = 0$ with initial values: $y(0) = 2, y'(0) = 1$

3. Solve a nonlinear equation:

$f'(t) = f(t)^2 + 1$

Plotting & Graphics

Plotting and graphing are techniques for visualizing mathematical functions. With Wolfram|Alpha, you can generate plots of functions, equations, and inequalities in one, two, and three dimensions. You can also explore different types of visualizations, such as polar plots, parametric plots, contour plots, and region plots, to gain a deeper understanding of the functions and equations you are interested in. For instance, you can use it to create a 3D plot of a surface, generate a parametric plot of a curve, or visualize the solutions to an inequality.

Plotting & Graphics Fields

Graph a function of one variable as a curve in the plane.

Functions

Plot a function of two variables as a surface in three-dimensional space.

3D Plots

Plot the solution set of an inequality or system of inequalities.

Inequalities

Plot a set of numbers or values on a real number line.

Number Lines

Draw a graph of points or curves in the polar coordinate system.

Polar Plots

Plot the solution set of an equation in two or three variables.

Equations

Graph parametric equations in two or three dimensions.

Parametric Plots

Examples:

1. Plot a function:

Plot: $x^3 – 6x^2 + 4x + 12$

2. Plot a region satisfying multiple inequalities:

Plot: $x^2 + y^2 leq$ and $y > x$

Numbers

Numbers are mathematical entities that were initially used to count objects and measure quantities. Over time, as the need for more general numeric entities arose, broader sets of numbers came into use, including tallying systems, counting numbers, integers, zero, rational numbers, irrational numbers, and complex numbers. Wolfram|Alpha’s computational knowledge can help you identify the properties of these number sets and perform calculations within and across their respective domains. For example, you can use it to find the prime factors of a number, convert a fraction to a decimal, or perform arithmetic with complex numbers.

Numbers Fields

Perform arithmetic with integers or compute properties about a particular integer.

Integers

Perform computations with or identify the properties of numbers that can be expressed as quotients of integers.

Rational Numbers

Perform computations with or identify the properties of numbers that cannot be expressed as quotients of integers.

Irrational Numbers

Check whether numbers are algebraic, compute the properties of algebraic numbers or find minimal polynomials of algebraic numbers.

Algebraic Numbers

Ask about nonalgebraic numbers.

Transcendental Numbers

Work with the set of numbers with real and imaginary parts.

Complex Numbers

Perform computations without sacrificing accuracy.

Arbitrary Precision

Learn about and utilize well-known constants from different areas of mathematics.

Mathematical Constants

Attempt to express approximate numbers using exact numbers, and vice versa.

Number Recognition

Convert numbers to and from different number bases and compute the results of a variety of bitwise, arithmetic and other operations in non-decimal number bases.

Base Conversions

Convert numbers to and from historical number systems.

Historical Numbers

Find a number name, determine properties of a named number or solve word problems containing named numbers.

Number Names

Find the most specific number type that encompasses all possible outputs from an expression involving general number types.

Number Type Arithmetic

Examples:

1. Compute a decimal approximation to a specified number of digits:
Approximate $pi$ to 1000 digits

2. Convert a decimal number to another base:
Convert 219 to binary

Trigonometry

Trigonometry is the study of the relationships between the side lengths and angles of triangles and their applications. This field is essential to mathematics, engineering, and various sciences. Wolfram|Alpha offers comprehensive tools for trigonometry, allowing you to compute values of trigonometric functions, solve trigonometric equations, and more. For example, you can use it to find the sine of an angle, solve a right triangle, or analyze wave functions.

Trigonometry Fields

Evaluate trigonometric functions or larger expressions involving trigonometric functions with different input values.

Trigonometric Calculations

Learn about and perform computations using trigonometric functions and their inverses, over the real or complex numbers.

Trigonometric Functions

Learn about and apply well-known trigonometric identities.

Trigonometric Identities

Study the relationships between side lengths and angles of triangles when these triangles are drawn atop a spherical surface.

Spherical Trigonometry

Solve equations involving trigonometric functions.

Trigonometric Equations

Learn about and apply well-known trigonometric theorems.

Trigonometric Theorems

Examples:

1. $sin(30^circ)$

2. $cos(pi/4)$

3. $tan(x) = 1$

4. $sec(45^circ)$

Linear Algebra

Linear algebra utilizes vector and matrix operations to study the properties of linear systems. Wolfram|Alpha’s extensive computational knowledge of topics like vectors, vector spaces, and matrix theory makes it a valuable resource for calculating and exploring the properties of vectors and matrices, determining the linear independence of vectors, and examining the vector spaces underlying sets of vectors and matrices. For instance, you can use it to solve a system of linear equations, perform matrix multiplication, or find the eigenvalues of a matrix.

Linear Algebra Fields

Find properties of and perform computations on n-dimensional vectors.

Vectors

Explore various properties of matrices.

Matrices

Check vectors for both linear dependence and linear independence.

Linear Independence

Compute properties of linear vector spaces.

Vector Spaces

Examples:

1. $begin{pmatrix} 1 & 2 \ 3 & 4 end{pmatrix}$

2. $text{Inverse of } begin{pmatrix} 1 & 2 \ 3 & 4 end{pmatrix}$

3. $begin{cases} 2x + 3y = 5 \ 4x – y = 6 end{cases}$

4. $begin{pmatrix} 1 & 2 \ 3 & 4 end{pmatrix} times begin{pmatrix} 5 & 6 \ 7 & 8 end{pmatrix}$

Number Theory

Number theory is a branch of mathematics that focuses on whole numbers and their properties. Key concepts include prime numbers, divisors, and Diophantine equations. Modern number theory has many applications, such as elliptic-curve cryptography and even music theory. For example, you can use it to find the greatest common divisor of two numbers, test a number for primality, or explore the solutions to a Diophantine equation.

Number Theory Fields

Primes are the building blocks of the naturals. Compute prime factorizations, find nth primes or make lists of primes.

Prime Numbers

Test if a number divides another, compute a number's divisors or find the greatest common divisor for a set of numbers.

Divisors

Solve equations with one or many unknowns, considering only integer solutions.

Diophantine Equations

Convert numbers between bases and compute the sum of their digits.

Digit Sums

Compute the finite or infinite continued fraction representations of numbers and functions.

Continued Fractions

Work with notable integers and classes of integers, such as the polygonal numbers and the binomial coefficients.

Special Numbers

Examples:

1. Prime factors of 56

2. Is 97 a prime number?

3. GCD of 48 and 180

4. LCM of 15 and 20

Discrete Mathematics

Discrete mathematics deals with areas of mathematics that are discrete, rather than continuous, in nature. This includes topics such as sequences and series, counting problems, graph theory, and set theory. Use Wolfram|Alpha to apply and understand these and related concepts. For example, you can use it to find the next term in a sequence, solve a combinatorial problem, analyze a graph, or explore the properties of sets.

Discrete Mathematics Fields

Use the ideas of permutation and combination to find binomial coefficients or integer partitions or to do other forms of counting.

Combinatorics

Work with known graphs or specify your own via adjacency lists. Check for isomorphism, compute the shortest path and more.

Graph Theory

Compute the properties of these discrete subsets of Euclidean space. Deal with regular or rooted lattices. Compare them.

Point Latices

Deduce patterns in incompletely specified sequences or series. Sum infinite series or perform other operations on them.

Sequences

Solve recurrences, specify initial values or attempt to model sequences with recurrences.

Recurrences

Work with the famous function known for being a total computable function that is not primitive recursive.

Ackermann Function

Examples:

1. How many ways can 5 people be seated in a row?

2. Number of subsets of a set with 8 elements

3. Shortest path in a graph using Dijkstra’s algorithm

4. $P rightarrow Q$

Complex Analysis

Complex analysis is the field of mathematics that studies complex numbers and functions of a complex variable. Wolfram|Alpha’s powerful computational tools enable you to perform complex arithmetic, analyze and compute properties of complex functions, and apply the methods of complex analysis to solve related mathematical problems. For example, you can use it to evaluate complex integrals, find residues of complex functions, or solve complex differential equations.

Complex Analysis Fields

Analyze properties of functions of a complex variable or perform basic arithmetic on, find roots of or apply functions to complex numbers.

Complex Numbers

Plot functions of a complex variable or compute and analyze their properties.

Complex Functions

Locate poles of a complex function within a specified domain or within the entire complex plane.

Poles

Compute the residues of functions in the complex plane at a point or within a specified region.

Residues

Compute and visualize Riemann surfaces for complex functions.

Riemann Surfaces

Examples:

1. Compute properties of a function of a complex variable (use the variable ????):

Compute: $e^z$

Evaluation: $e^{ipi} = -1$

2. Compute the residue of a function at a point:

Compute the residue of $frac{1}{(z^2+4)^2}$ at $z=2i$

Applied Mathematics

Applied mathematics is the branch of mathematics focused on using mathematical results, techniques, and methods, along with specific subject-area expertise, to understand and solve real-world problems in science, technology, business, society, engineering, and industry. Wolfram|Alpha’s extensive computational knowledge and powerful mathematical algorithms enable you to apply mathematical techniques to compute, analyze, and explore various practical problems. For example, you can use it to optimize business processes, model scientific phenomena, or analyze engineering systems.

Applied Mathematics Fields

Find global and local extrema and stationary points of functions or impose a constraint on a function and compute the constrained extrema.

Optimization

Use numerical analysis to compute roots of equations, to solve numerical integrals and to solve ordinary differential equations.

Numerical Analysis

Use Wolfram|Alpha to explore discrete- and continuous-time dynamical systems and control systems.

Dynamical Systems

Ask about fractals both over real and complex domains.

Fractals

Estimate the number of objects required to pack or cover another object.

Packaging & Covering Objects

Get information about and analysis of the risks and rewards of cooperation and conflict in a variety of mathematical games.

Game Theory

Examples:

1. Minimize or maximize a function:

Maximize $x(1-x)e^x$

2. Numerically integrate functions that cannot be integrated symbolically:

Integrate: $int sin(x) cos(x) , dx text{ from } 0 text{ to } 1$

Logic & Set Theory

Symbolic logic and set theory are foundational to mathematics and are deeply interconnected. Use Wolfram|Alpha to visualize, compute, and transform logical expressions or terms in Boolean logic or first-order logic. Wolfram|Alpha can also create tables and diagrams, perform set-theoretic operations, and compute set theory predicates such as equality and subsets. For example, you can use it to simplify a logical expression, generate a truth table, find the intersection of sets, or verify if one set is a subset of another.

Logic & Set Theory Fields

Compute truth tables, find normal forms and construct logic circuits for any Boolean expression of any number of Boolean variables.

Boolean Algebra

Test for set membership, set equality and subset relations. Draw a Venn diagram for a moderate number of sets.

Set Theory

Perform arithmetic operations and simplify expressions involving infinite cardinals. Test cardinal numbers for cardinal equality or explore cardinal inequality.

Transfinite Numbers

Examples:

1. Compute a truth table:

Truth Table: $P & (Q | R)$

2. Generate a Venn diagram:

Venn Diagram: $ (text{complement } S) cap (A cup B)$

Mathematical Functions

In mathematics, a function is a relation, numerical or symbolic, between a set of inputs (the function’s domain) and a set of potential outputs (the function’s codomain). The power of the Wolfram Language enables Wolfram|Alpha to compute properties for both user-defined functional forms and hundreds of known special functions. Use our extensive functionality to compute properties like periodicity, injectivity, and parity for polynomial, elementary, and other special functions. For example, you can use it to determine if a function is periodic, check if it is injective (one-to-one), or find its parity (odd or even).

Mathematical Functions Fields

Compute the domain and range of a mathematical function.

Domain & Range

Determine the injectivity and surjectivity of a mathematical function.

Injectivity & Surjectivity

Determine the continuity of a mathematical function.

Continuity

Determine the continuity of a mathematical function.

Continuity

Compute the period of a periodic function.

Periodic Functions

Determine the parity of a mathematical function.

Even & Odd Functions

Compute properties of multiple families of special functions.

Special Functions

Get information about arithmetic functions, such as the Euler totient and Möbius functions, and use them to compute properties of positive integers.

Number Theoretic Functions

Compute alternative representations of a mathematical function.

Representation Formulas

Examples:

1. Do computations with special functions:

Compute: $frac{d}{dx} sin(x^2)$

2. Do computations with number theoretic functions:

Compute: $phi(110)$

Mathematical Definitions

Wolfram|Alpha has access to a vast collection of knowledge on mathematical objects, expressions, and theorems. It can identify the mathematical subject of a given concept according to its Wolfram MathWorld subject category and its MSC 2010 classification code, and find related topics based on this categorization. For example, you can use it to categorize a mathematical theorem, look up its classification code, and explore related theorems or concepts within the same category.

Mathematical Definitions Fields

Find properties of a mathematical term.

Mathematical Definitions

Learn about the classification of a mathematical subject and find related topics.

Mathematical Subjects

Examples:

1. Find information about a math concept:

Explain a tangram in mathematics.

2. Get a brief definition:

Explain what prime numbers are.

Famous Math Problems

Throughout history, many famous math problems were posed that could not be solved at the time. Some conjectures lasted for hundreds of years before being proven or disproven, and some remain unsolved. Wolfram|Alpha has knowledge of many of these renowned math problems, including Hilbert’s 23 problems and the Millennium Prize problems. For example, you can use it to learn about the Riemann Hypothesis, explore the history of Fermat’s Last Theorem, or delve into the details of the Poincaré Conjecture.

Famous Math Problems Fields

Find information about an unsolved math problem.

Open Conjectures

Find information about a solved problem.

Solved Problems

Examples:

1. Get information about a mathematical conjecture:

Conjecture: Riemann Hypothesis

2. Get historical information about a theorem:

Theorem: Fermat’s Last Theorem

Continued Fractions

The continued fraction representation of a number is a sum of two terms. The first term is the integer part of the number, and the second term is recursively defined as the reciprocal of the continued fraction form of the reciprocal of the number’s fractional part. Rational numbers can be represented by finite continued fractions, while irrational numbers require infinitely deep representations. Wolfram|Alpha can convert between these representations and utilize them. It also possesses knowledge about symbolic continued fractions and related theorems and algorithms. For example, you can use it to find the continued fraction of a rational number, approximate an irrational number with a continued fraction, or explore the properties and theorems related to continued fractions.

Continued Fractions Fields

Convert between decimal and continued fraction representations of numbers.

Numbers

Convert between regular and continued fraction representations of functions.

Functions

Learn about the meanings of terms and phrases relevant to the area of continued fractions.

Definitions of Terms

Learn about theorems related to continued fractions. Apply them and see where and how they are applied.

Theorems

Learn about and use different algorithms for finding and working with continued fraction representations.

Algorithms

Search for literature relevant to the area of continued fractions.

Literature

Examples:

1. Find the continued fraction representation of a number:

Number: ????

Representation: $[3;7,15,1,292,…]$

2. Find definitions of continued fraction terminology:

What does the term “Regular Continued Fraction” mean?

Statistics

Statistics is the branch of mathematics focused on collecting, analyzing, and presenting data. Given a set of data, Wolfram|Alpha can instantly compute various descriptive and inferential statistical properties, perform regression analyses, and fit equations. Wolfram|Alpha’s extensive computational knowledge of statistical methods allows you to analyze, interpret, and visualize your data quickly and accurately. For example, you can use it to calculate the mean and standard deviation of your data, perform a t-test, generate a linear regression model, or create visualizations like histograms and scatter plots.

Statistics Fields

Compute statistical measures that summarize the properties of a dataset.

Descriptive Statistics

Use statistics and hypothesis tests to infer information from a dataset.

Statistical Inference

Fit different parameterized models to data.

Regression Analysis

Compute the probability of a random variable returning a specified value or falling within a range of values or determine the expected value of a random variable.

Random Variables

Examples:

1. Calculate basic descriptive statistics for a data set:

Data set: ${25, 35, 10, 17, 29, 14, 21, 31}$

Calculate: Mean, Median, Standard Deviation

2. Find the sample size needed to estimate a binomial parameter:

Parameter: Sample size for binomial parameter

Probability

Probability is the quantification of the likelihood that an event or a set of events will occur. Using Wolfram|Alpha’s extensive computational understanding of probability and its expansive knowledge of real-world applications, you can compute the chances of winning various games driven by random chance, conduct and analyze the outcomes of random trials, visualize and compute the properties of probability distributions, and calculate the probabilities of events given a set of conditions. For example, you can use it to find the probability of rolling a specific number with a die, simulate the results of a coin toss experiment, analyze a normal distribution, or determine the likelihood of drawing a specific card from a deck.

Probability Fields

Compute winnings, analyze bets and determine outcomes for games of chance ranging from the toss of a coin to a game of poker and the draw of your local lottery numbers.

Games of Chance

Determine the likelihood of any outcome for any number or specification of Bernoulli trials.

Bernoulli Trials

Compute the chance people in a group have of sharing a birthday or investigate the likelihood of people's birthdays falling in a specific date range or month or on a specific day of the week.

Birthday Probabilities

Compute the probabilities of various compositions of events or specify individual probabilities to determine the likelihood of some, all or no events occurring.

Probability Formulas

Compute a specific property of a probability distribution, the likelihood that an outcome has of occurring or explore the defining characteristics of a vast set of probability distributions.

Probability Distributions

Examples:

1. Compute the probability of a union of events:

Events: probability of the union of three events

2. Compute coin-toss probabilities:

Compute the probability distribution of heads and tails for 32 coin tosses

Common Core Math

The Common Core State Standards (CCSS) for Mathematics outline the mathematical content to be taught in the United States from kindergarten through high school. Released in 2010 by a state-led coalition of educators and content experts, these standards have been adopted by 41 states, the District of Columbia, Guam, the Northern Mariana Islands, and the US Virgin Islands. The CCSS are a comprehensive list of topics that build on each other across grade levels, emphasizing conceptual understanding and real-world applications alongside mathematical procedures. These standards serve as a framework for educators to provide all students in the United States with rigorous mathematics instruction.

The Common Core math example pages, organized by grade level and content area, showcase how Wolfram|Alpha can support K–12 math students and teachers. Wolfram|Alpha offers tools for mathematical computation that not only affirm traditional education models but also incorporate the integrated, rigorous approach of the CCSS. For example, students can use Wolfram|Alpha to solve algebraic equations, visualize geometric shapes, analyze statistical data, and explore calculus concepts, all in alignment with the CCSS.

Common Core Math Fields

Get information about kindergarten math Common Core Standards, which cover counting and categorizing objects.

Kindergarten

See examples aligned to first grade math Common Core Standards, including adding and subtracting whole numbers and measuring lengths.

Grade 1

Explore problems that demonstrate second grade math Common Core Standards, such as solving equations and partitioning shapes.

Grade 2

Discover content covered in third grade math Common Core Standards, including multiplication and fractions.

Grade 3

Get information about fourth grade math Common Core Standards, which cover angle measurements and all four arithmetic operations.

Grade 4

See examples aligned to fifth grade math Common Core Standards, such as plotting points and evaluating expressions.

Grade 5

Explore problems that demonstrate sixth grade math Common Core Standards, which cover data analysis and solving algebraic equations.

Grade 6

Discover content covered in seventh grade math Common Core Standards, including ratios, percentages and probability.

Grade 7

Get information about eighth grade math Common Core Standards, which cover exponents and irrational numbers.

Grade 8

Explore content covered in high school math Common Core Standards, including functions, statistics and trigonometry.

High School

See examples aligned to the Operations & Algebraic Thinking Common Core Standards, designed to help students explore the four arithmetic operations.

Algebraic Thinking

Explore problems that demonstrate the Counting & Cardinality Common Core Standards, such as counting groups of up to 20 objects.

Counting & Cardinality

Discover content covered in the Expressions & Equations Common Core Standards, including simplifying and solving equations and inequalities.

Expressions & Equations

Get information about the Number & Operations—Fractions Common Core Standards, which cover performing arithmetic operations with fractions and representing fractions visually.

Fractions

See examples aligned to the Functions Common Core Standards for eighth grade, in which students identify and analyze linear functions.

Functions

Explore problems that demonstrate the Geometry Common Core Standards, in which students define shapes and their geometric properties.

Geometry

Discover content covered in the Measurement & Data Common Core Standards, including measuring objects and converting between units of measure.

Measurement & Data

See examples aligned to the Number & Operations in Base Ten Common Core Standards, in which students build an understanding of place value.

Numbers in Base Ten

Explore problems that demonstrate the Number System Common Core Standards, such as performing operations with rational numbers and plotting ordered pairs.

Number System

Get information about the Ratios & Proportions Common Core Standards, including computations with percentages and unit rates.

Ratios & Proportions

See examples aligned to the Statistics & Probability Common Core Standards, in which students analyze and display data.

Statistics & Probability

Explore problems that demonstrate the High School Algebra Common Core Standards, such as solving equations and factoring polynomials.

High School Algebra

See examples aligned to the High School Functions Common Core Standards, in which students describe and analyze function behavior.

High School Functions

Discover content covered in the High School Geometry Common Core Standards, including defining geometric objects algebraically and proving geometric theorems.

High School Geometry

Get information about the High School Number & Quantity Common Core Standards, including computing with exponents, vectors and complex numbers.

High School Number & Quantity

Explore problems that demonstrate the High School Statistics & Probability Common Core Standards, such as describing datasets and computing probabilities.

High School Statistics & Probability

Examples:

1. Evaluate an expression (CCSS.Math.Content.6.EE.A.2c):

Evaluate the expression: $text{if } x = 4, text{ what is } 3x + 5?$

2. Perform multiple operations with rational numbers (CCSS.Math.Content.7.NS.A.2c):

Expression: $-1/2 + 3/8 + 1/4 + -3/2$

Science & Technology

Students and teachers can access WolframAlpha’s extensive knowledge related to science and technology. Utilizing its powerful computational capabilities, this integration allows users to solve problems in physics, chemistry, engineering, computational sciences, and many other domains.

Physics

Physics studies the features of the universe, encompassing both natural and man-made phenomena. With Wolfram|Alpha, you can explore data on topics such as quantum mechanics, nuclear and particle physics, thermodynamics, and Newtonian mechanics.

Wolfram|Alpha also provides a wealth of physical formulas and constants. This built-in data and the interactive calculators make it easy to get answers to your physics questions, whether for homework or general curiosity.

For example, you can use it to calculate the energy levels in a hydrogen atom, determine the efficiency of a heat engine, analyze the motion of a projectile, or find the half-life of a radioactive substance.

Physics Fields

Explore the physical laws that describe the behavior of one or more bodies under a system of forces.

Mechanics

Explore oscillatory motion, from pendulums to electromagnetic waves.

Oscillations & Waves

Explore the motion of fluids using statistical methods.

Statistical Physics

Explore heat, energy and entropy and how they relate to thermodynamic systems.

Thermodynamics

Explore the physics of the electromagnetic force.

Electricity & Magnetism

Study the properties and behaviors of light.

Optics

Explore Einstein's theories of special and general relativity and how they relate to gravity, time and space.

Relativity

Explore aspects of nuclear physics, including radiation and nuclear power.

Nuclear Physics

Explore quantum phenomena, such as scattering and quantum states.

Quantum Physics

Get information about particles and their interactions.

Particle Physics

Explore the nature of celestial objects, including black holes, stars and planets.

Astrophysics

Explore details, values and definitions for various physical constants.

Physical Constants

Explore physical laws, principles and effects.

Physical Principles

Get information on physical effects and compare them.

Physical Effects

Examine the behavior of fluid systems and objects moving through them.

Fluid Mechanics

Examples:

1. Compute mechanical work:

F = 30 N, d = 100 m

2. Compute the photon energy given wavelength:

( lambda ) = 435 nm

Chemistry

Chemistry is the study of matter, from individual atoms and ions to large biomolecules. With Wolfram|Alpha, you can explore data about chemical compounds, the reactions they undergo, solubility, and chemical graph theory. It also provides information on chemical quantities, unit conversions, molarity calculations, and stoichiometry.

Use Wolfram|Alpha to answer your chemistry questions, whether for homework or general curiosity. For example, you can calculate the molar mass of a compound, balance chemical equations, determine the solubility of a substance, or convert between different units of measurement.

Chemistry Fields

Use Wolfram|Alpha to explore the elements of the periodic table.

Chemical Elements

Search for chemicals by name, chemical formula or other identifier.

Molecules

Learn about positively and negatively charged ions and their properties.

Chemical Ions

Compute extensive properties for chemicals, which depend on the amount of substance present, and convert quantities between different units.

Chemical Quantities

Compute thermodynamic properties such as entropy, heat capacity or vapor pressure for a wide variety of chemicals.

Chemical Thermodynamics

Explore properties of different solutions, which depend on the solvent, solute and concentration.

Chemical Solutions

Explore functional groups such as cyanates, peroxides, alkanes and halides.

Functional Groups

Use Wolfram|Alpha to explore cheminformatics properties from graph invariants like Balaban's J index or the Hosoya index to QSAR descriptors like the hydrogen donor count or the longest chain.

Cheminformatics

Connect chemical properties with the underlying quantum mechanical nature of atoms and molecules.

Quantum Chemistry

Explore properties of electronic orbitals and the bonds they form. Find bonds by their constituent atoms, by their bond type or by the parent chemical.

Bonds & Orbitals

Investigate nuclear chemistry with Wolfram|Alpha.

Nuclear Chemistry

Explore physical laws, principles and effects.

Physical Principles

Examples:

1. Get information about the chemical element carbon.

2. Balance the following chemical equation:

$text{Al} + text{O}_2 rightarrow text{Al}_2text{O}_3$

Units & Measures

Wolfram|Alpha can find and convert values for a wide variety of units, measures, and scales. You can find information and convert between standard industrial measures, scientific scales, everyday life units, and many others.

For example, you can use it to convert between metric and imperial units, find the equivalent of a temperature in different scales, convert currency values, or determine the energy content of different foods.

Whether you need precise scientific measurements or everyday conversions, Wolfram|Alpha provides the tools to get accurate results.

Units & Measures Fields

Examine unit values and conversions between different units.

Units

Associate physical quantities with the devices used to measure them.

Measurement Devices

Convert footwear and jewelry sizes to sizes used in other countries.

Fashion Sizes

Estimate the number of objects needed to cover or fill a given region.

Packing & Covering Objects

Convert industrial measures used for wires, screws, bolts and other objects to common units.

Industrial Measures & Standards

Retrieve detailed data on physical quantities and dimensionless quantities. Determine dimensionless combinations of physical quantities.

Physical Quantities

Examples:

1. Get unit conversions for a quantity:
Convert: 120 meters

2. Estimate the number of objects required to fill a container:
How many baseballs fit in a Boeing 747?

Engineering

Engineering is a discipline that deals with the design, construction, analysis, and maintenance of structures, machines, and systems using scientific methods, mathematical knowledge, and physical principles. It encompasses many fields and disciplines, from mechanical and structural to chemical and aerospace engineering.

Wolfram|Alpha allows you to explore various facets of engineering, including computing formulas and constants for electricity, materials science, aerodynamics, and more.

For example, you can use it to calculate electrical resistance, analyze the stress and strain on materials, determine lift and drag forces in aerodynamics, or solve chemical reaction equations in chemical engineering.

Engineering Fields

Explore data about aircraft, rockets, satellites or space probes.

Aerospace Engineering

Look up data regarding the global energy industry, including production, consumption and prices.

Energy Data

Explore the applications of the electromagnetic force for various practical purposes.

Electrical Engineering

Compute, analyze and plot properties of models that represent the behavior of control systems.

Control Systems

Look up information regarding mechanical engineering formulas and constants for topics including refrigeration and materials science.

Mechanical Engineering

Calculate the forces on structures, such as bridges and buildings, that we use every day.

Civil Engineering

Look up details and formulas of fluid mechanics, including pressure, buoyancy and fluid flow.

Fluid Mechanics

Explore the science and applications of sound and acoustics. See how waves interact with liquids, solids and gases.

Sound & Acoustics

Compute the properties of steam, saturated steam and phase boundaries.

Steam Tables

Look up information about measuring devices, including things like name, precision and range.

Measurement Devices

Examples:

1. Compute magnetic flux density for an object:

Compute the magnetic flux density given the following: 1 $A$ in a 1 $m$ Helmholtz coil

2. Compute the maximum force of a spring:

What is the maximum force of a spring with: k = 200 $N/m$, x = 0.1 $m$?

Earth Sciences

Earth science is the collection of domains that involve the study of Earth and its atmosphere. It includes environmental disciplines and concepts such as geology, geodesy, oceanography, atmospheric studies, and climatology.

For example, you can explore topics like the structure of Earth’s interior, the measurement and representation of Earth’s shape, the dynamics of ocean currents, weather patterns and forecasting, and the long-term trends in climate.

Wolfram|Alpha provides tools and data to help you understand and analyze these various aspects of Earth science.

Earth Science Fields

Explore the geology of Earth, including its structure, history and composition.

Geology

Navigate various coordinate systems and explore physical properties of the globe.

Geodesy & Navigation

Obtain locations and other characteristics of the world's oceans.

Oceanography

Get information about the Earth's atmosphere.

Atmospheric Sciences

Gain an understanding of the Earth's climate from a variety of relevant data.

Climate

Examples:

1. Get information about one of the Earth’s geological layers:

What is the asthenosphere?

2. Compute the saturation vapor pressure:

What is the saturation vapor pressure at 30$^{circ}$C

Transportation

Transportation describes the movement of cargo or passengers to and from various locations. Use Wolfram|Alpha to investigate a diverse set of transportation concepts, including transportation centers, pathways, and formulas.

For example, you can explore data on major transportation hubs like airports and seaports, analyze the shortest paths or optimal routes between locations, calculate fuel efficiency and travel time, and examine the logistics of cargo transport.

Wolfram|Alpha provides the tools to help you understand and optimize various aspects of transportation systems.

Transportation Fields

Discover the extent of roads, which are among the most-used forms of transportation for passengers and cargo.

Road Transport

Obtain an understanding of air transportation of passengers and cargo.

Air Transport

Study the extent and capacity of rail transport systems.

Rail Transport

Gain an understanding of water transport systems, which use ships to transport goods and people.

Water Transport

Query for data on rockets, which are the primary method used for space transport.

Space Transport

Examples:

1. Get information about an automobile model:

Write all the specifications for the Mini Cooper Roadster.

2. Do computations on airline data:

What are the average amount of daily passengers on Union or Delta?

Computational Sciences

Compute properties of abstract machines in computational sciences, the branch of science studying computers and their use.

Examples:

1. Compute properties of an elementary cellular automaton:

Rule 110

2. Compute properties of a Turing machine:

What are the properties of a Turing machine 2506?

Materials

Explore properties of a range of materials from minerals to man-made alloys and plastics.

Examples:

1. Get information about an alloy:

Provide information about the alloy, carbon steel.

2. Convert a specific material hardness to various other systems:

Convert Mohs 6.5 to various other systems

Space & Astronomy

Investigate a range of topics involving space and astronomy, from celestial objects and astronomical events to manned space missions and space probes.

Examples:

1. Compute the date and properties of an eclipse:

When is the next solar eclipse?

2. Convert a specific material hardness to various other systems:

Convert Mohs 6.5 to various other systems

Life Sciences

Life science deals with the diverse aspects of living organisms, ranging from genetics to the analysis of molecular, cellular and tissue components to the biological classification of groups of organisms. Wolfram|Alpha provides information about genomics, molecular biology, human anatomy, neuroscience and individual animals and plants.
Examples:
1. Compute the date and properties of an eclipse:
When is the next solar eclipse?
2. Convert a specific material hardness to various other systems:
Convert Mohs 6.5 to various other systems

Pro Membership

Get factual information every time with the Wolfram|Alpha integration. No matter which subject you’re studying (or teaching), our WolframAlpha integration gives you superpowers!